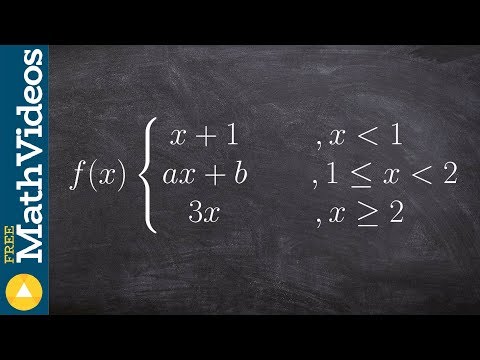F X X2 4 X 2 If X 2 Ax2 Bx 1 If 2 X 3 4x A B If X 3
Factor the expression by grouping.
F x x2 4 x 2 if x 2 ax2 bx 1 if 2 x 3 4x a b if x 3. Tap for more steps. It is pretty strait forward if you follow all the. Tap for more steps.
Vii x 2 3 2x x2 1 x3 8 x2 12x 2x3 2x x3 14x 6x2 8 0 it is not of the form ax2 bx c 0. Answer to find the values of a and b that make f continuous everywhere f x x2 4x 2 if x 2 ax2 bx 3 if 2 x. Related symbolab blog posts.
High school math solutions quadratic equations calculator part 3. The value of a and b are 3 and 1 respectively. Complete the square for.
The graph of any quadratic function has the same general shape which is called a parabola the location and size of the parabola and how it opens depend on the values of a b and c as shown in figure 1 if a 0 the parabola has a minimum point and opens upward if a 0 the parabola has a maximum point and opens downward. Given that x 2 is a factor of polynomial. To find a and b set up a system to be solved.
Find the properties of the given parabola. Found 3 solutions by richard1234 stanbon valeriedavis. Consider the vertex form of a parabola.
Hence the given equation is not a quadratic equation. Hence the given equation is not a quadratic equation. Vi x2 3x 1 x 2 2 x2 3x 1 x2 4 4x 7x 3 0 it is not of the form ax2 bx c 0.
On the last post we covered completing the square see link. F x x2 4x 2 if x2 ax2 bx 3 if 2 x3 2x a b if x 3 i dont understand how i would solve this. Also when divided by x 3 leaves a remainder 3.
Solve your math problems using our free math solver with step by step solutions. First the expression needs to be rewritten as x 2 ax bx 3. Rewrite the equation in vertex form.
Find the values of a and b that make f continuous everywhere. We have to find the value of a and b. The function f x ax 2 bx c is a quadratic function.
Our math solver supports basic math pre algebra algebra trigonometry calculus and more. Use the form to find the values of and. As 2 is the zero of the polynomial therefore by remainder theorem 1.